Rastreando la evolución.

Uno de los principales objetivos de la Biología como campo de estudio es entender cómo funciona el motor de la diversidad en nuestro planeta: la Evolución. Esta es la razón por la que dentro de este campo encontramos a "biólogos evolutivos" (término que siempre me ha parecido redundante), que se especializan en estudiar los mecanismos por los que dicho proceso se rige. Por otro lado tenemos a casi todos los demás, que nos dedicamos en mayor o menor medida a estudiar los resultados de dicha evolución. Sin embargo, un pequeño grupo de biólogos (y geólogos) trabajan en intentar reconstruir los pasos que ha dado esta a lo largo del tiempo y así rastrear la relación entre los seres vivos.



Muchos conocemos el trabajo realizado por los paleontólogos, que ha arrojado luz sobre grandes incógnitas y que siempre han sido una de las bases más sólidas de la Teoría Evolutiva. Sin embargo, con la revolución genómica y el desplome del coste de la secuenciación cada vez tenemos más y más información sobre genes de diferentes especies, lo que nos ofrece por primera vez la posibilidad de estudiar qué cambios se han producido en el lugar donde estos cambios importan, y por tanto podemos establecer relaciones e incluso estimar cómo eran los ancestros comunes de las especies que tenemos hoy en día. Todo esto suena genial, verdad? Pues sí, mola mucho, pero cómo se hace?

El primer paso es secuenciar el genoma, obviamente. Podéis encontrar una descripción excelente de este proceso por Guillermo Peris (@waltzing_piglet) en su blog en Naukas, y como no lo voy a hacer mejor, os dejo con ella. Una vez tenemos una secuencia de consenso a partir de todos los fragmentos secuenciados, debemos alinear estas secuencias. Existen una enorme cantidad de algoritmos para hacer esto, y dependiendo de lo que queramos y de las características de nuestras secuencias unos son mejores que otros, pero la idea básica es que necesitamos que el ordenador empareje nuestras secuencias de ADN de forma que podamos comparar donde ha habido cambios.




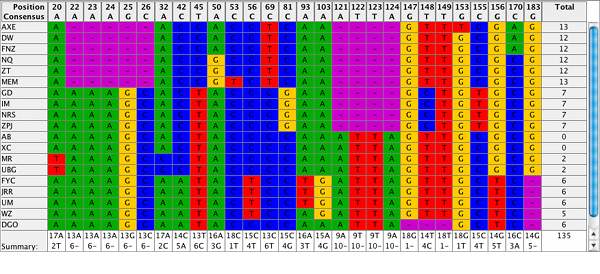
Como podemos ver es la imagen superior, este alineamiento incluye también huecos donde el ADN se ha perdido o donde ADN nuevo se ha insertado (deleciones e inserciones, respectivamente, aunque normalmente se las llama directamente indels). Esto obviamente complica bastante el alineamiento, y por tanto la elección del algoritmo que usamos es bastante importante.

Una vez que tenemos el alineamiento realizado, podemos usar bastantes modelos estadísticos para poder estimar la relación genética entre las secuencias. Y posiblemente os preguntaréis por qué, si ya tenemos las secuencias alineadas y por tanto podemos contar las diferencias. Y tenéis razón, podemos. Este modelo, conocido como Máxima Parsimonia, presupone que, para llegar a donde estamos, se han producido el número mínimo de cambios, y por tanto no hacen falta grandes modelos estadísticos.



Sin embargo, este modelo suele ser demasiado simplista, pues siempre tenemos la posibilidad de que una mutación suceda en una posición que ya había mutado anteriormente. A más tiempo (y mutaciones), mayor la probabilidad de que esto pase. Por tanto, necesitamos un modelo que considere estas mutaciones "superpuestas".

Dentro de estos modelos encontramos algunos que consideran que todas las mutaciones son igual de probables (Jukes-Cantor), que hay diferentes frecuencias entre transiciones y transversiones (Kimura), o que hay frecuencias diferentes dependiendo de la base (HKY o GTR).




Y si todo esto no fuese suficiente lío, todavía tenemos que ver qué tipo de algoritmos usamos, porque hay un montón. Sin embargo, todos ellos pueden agruparse en tres tipos, dependiendo de en qué métrica se basan:

• Métodos de Distancia: A partir de nuestro alineamiento y con un modelo seleccionado podemos calcular la distancia (la cantidad de cambios estimada por el modelo) que hay entre las diferentes secuencias para construir lo que se conoce como una Matriz de Distancias. Una vez tenemos dicha matriz, podemos usar uno de los algoritmos de este grupo para construir un árbol filogenético.
• Máxima Verosimilitud (Maximum Likelihood): Estos métodos se basan en la matriz de verosimilitud, que evalúa el ajuste de cada secuencia a una secuencia modelo, obteniendo así una métrica similar a la distancia. A partir de aquí, el algoritmo elegido (que hay varios) inferirá la distribución de probabilidad de los posibles árboles, eligiendo el (o los) más probable. 
• Modelos Bayesianos: Si la anterior os parecía complicada, esta lo es todavía más, pues usa una simulación conocida como Markov Chain Monte Carlo sampling simulation para simular una serie de cambios circulares y así estimar la distribución de probabilidad de los árboles filogenéticos. Sin embargo, a diferencia de con los métodos de Máxima Verosimilitud, aquí lo que hacemos es partir de una distribución original (prior, o a priori), que ponderamos con la de nuestros datos para estimar la distribución final (posterior, o a posteriori). 

Para terminar de rematar, todos estos métodos son increíblemente costosos a nivel de computación (hablamos de costosos nivel superordenador trabajando durante días o semanas), por lo que a todo este follón estadístico hay que añadir algoritmos que nos permitan buscar posibles árboles sin tener que revisar todas y cada una de las posibilidades, en lo que se conoce como Búsqueda Heurística.

Como ya habréis podido intuir, este es un campo que requiere mucha prueba y error y tiene detrás un follón estadístico importante, pero espero haberos dado una pequeña idea general de qué hay detrás de esos árboles filogenéticos. Por último, me gustaría listar otras aplicaciones bastante interesantes para este tipo de análisis, que suelen pasar bajo el radar de mucha gente:

• Epidemiología: el análisis filogenético de bacterias y virus es una herramienta clave para saber si los casos de una región están relacionados con otra o si tenemos un nuevo brote. Además, podemos rastrear el origen de dicho brote hasta su reservorio (por ejemplo, con los virus del Ébola hasta los murciélagos de la fruta o el Lassa hasta los roedores del género Mastomys). 

• Paleogenética y genética de poblaciones: analizar la relación de las secuencias de ADN de muestras antiguas (hasta de otras especies de homínidos) nos está permitiendo comprender mucho mejor cómo nos hemos ido desarrollando como especie, hasta el punto en que ha dado lugar a un campo nuevo, conocido como Bioarquelogía. Además, esto no solo se aplica a nuestra especie: hay trabajos súper interesantes que se están llevando a cabo en perros, mamuts, leones...